为什么适用 CNN
相较于 DNN,CNN 使用局部连接和权值共享大大降低了参数量,为什么这种方法可行呢?
- 某一张图片的 pattern 通常只是一小部分,因此对于某一个神经元来说,并不需要看整张图像 (局部连接)

对于某一个局部特征,当他出现在图像的不同位置时,完全可以只使用一个 detector (权值共享)

对一张图像进行 subsampling,例如把奇数行、偶数列的 pixel 拿掉,并不会影响人们对这张图象的理解。而这却可以大大的降低计算量 (池化)
杂记
李宏毅老师的 PPT 真的讲的很仔细,把之前自学的一些疑惑点以及搞了很久才弄懂的东西很通俗易懂的讲出来了,这里简单记录一下。
彩色图像
彩色图像有 RGB 三个通道,但是其输出层的神经元个数仍然与卷积核的个数相等,每一个卷积核都与 iamge 的三层做内积。
CNN vs 全连接

局部连接和权值共享在这个图中已经显示的很清楚了
局部连接:全连接网络的后一个神经元与前一层所有神经元相连。而卷积操作中某一个神经元只连接了前一层的部分神经元,这一部分也成为感受野
权值共享:对于同一个卷积核得到不同的神经元,虽然他们连接了前一层中不同的神经元,但是所用到的权值都是一样的。
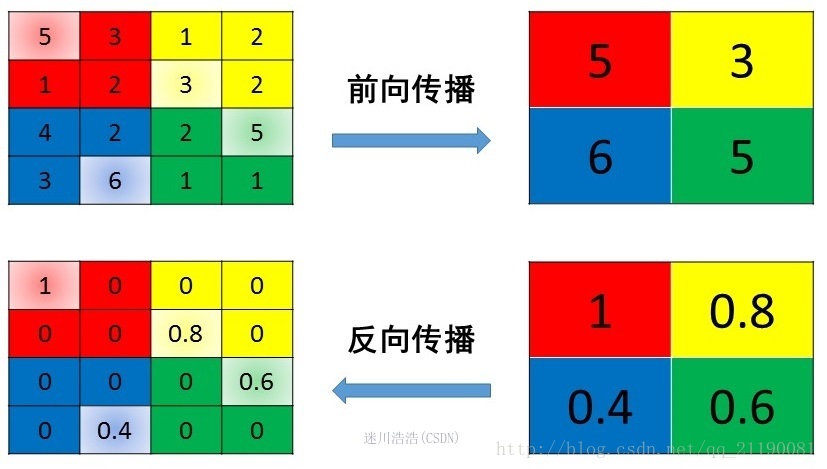
最大池化
池化操作看起来是不能微分的,一种比较直观的想法是把求得的梯度复制到池化窗口的每一个区域,这种操作会造成 loss 的总和是原来的 n 倍,极易产生梯度爆炸的现象。因此,正确的操作是把当前的梯度复制到池化窗口的某一个位置,而其他位置的梯度,就是 0。
Flatten
flatten 就是把 feature map 拉直,拉直之后就可以丢到全连接网络中(所以 CNN 中的全连接就像是集合了所有提取到的特征做分类),然后就结束了。
CNN 是如何工作的?
what does filter do
我们用 $a_{ij}^{k}$ 表示第 k 个卷积核下标 ij 分别表示第 i 行第 j 列,可以定义第 k 个卷积核的激活度可以表示为:
$$
a^k=\sum_{i=1}^{11}\sum_{j=1}^{11}a_{ij}^{k}
$$

在训练阶段,我们通过计算梯度来调整卷积核的参数使得损失尽量小。类似的,我们通过梯度上升来找到一张 image 使得这个卷积核的激活程度达到最大值,优化的目标表示如下:
$$
x^*=\arg\max_x a^k
$$
最终得到的结果如上图所示。以第三张 image 为例,上面布满了小小的斜条纹,可以认为其就是检测原图像中某个小部分的斜条纹这一特征。其他的卷积核也类似的检测输入图像的一些纹理特征。
what does neuron do
与上述方法类似的,我们也可以定义出最后的 flatten 操作中每个神经元的优化目标:
$$
x^*=\arg\max a^j
$$
最终得到的结果如上图所示。可以看到和 filter 得到的结果有很大的区别,因为在 flatten 之后,每个神经元所关注的不再是类似于 fliter 的某个部分,而是整张图片,所以图中所示就是可以使得他激活成都最大的 image。
what about output
类似的,我们以可以得到输出层神经元所最希望 “看到的” image。以手写数字识别为例,很自然的想法是如果以数字 1 所代表的输出去进行梯度上升,得到的图像应该是一个数字 1 的图形,但是最终的结果并不是这个样子的。神经网络所学到的东西跟我们一般人类的想象认知并不是完全一样的。当然,我们可以通过对网络添加一些限制来使得这个结果更加的趋近于数字。

应用
Deep Dream
把某一层的 filter 中的正值调大,负值调小,这样相当于 “夸大 CNN 所看到的信息”
Deep Style

Playing Go
Speech

Text