李宏毅深度学习笔记 6 - 半监督学习

什么是半监督学习

Supervised Learning：$(x^r,y^r)^R_{r=1}$

每一组 data 都有 input $x^r$ 和 output $y^r$ 相对应

Semi-supervised Learning：$\begin{Bmatrix}(x^r,\hat{y}^r)\end{Bmatrix}^R_{r=1}+\begin{Bmatrix}x^u\end{Bmatrix}^{R+U}_{u=R}$

部分 data 没有与 input $x^u$ 相对应的标签
实际上 data 很容易搜集，只是缺少有 label 的 data，所以 $U\ll R$

半监督学习是怎么工作的

没有标签的数据虽然只有 input，但是他们的分布，可以告诉模型进行分界线的调整。半监督学习的使用往往会伴随着假设，假设的合理与否，决定了最终结果的好坏。

————————————————

半监督生成模型

在有监督学习的概率生成模型中，以二分类为例，我们很容易就能得到 $P (C_1)$ 和 $P (C_2)$，通过对已知样本计算极大似然估计就能求得每个类别的均值和方差，从而可以得到 $P (x|C_1)$ 和 $P (x|C_2)$。最后根据概率公式就能计算出新的样本属于每个类别的概率。

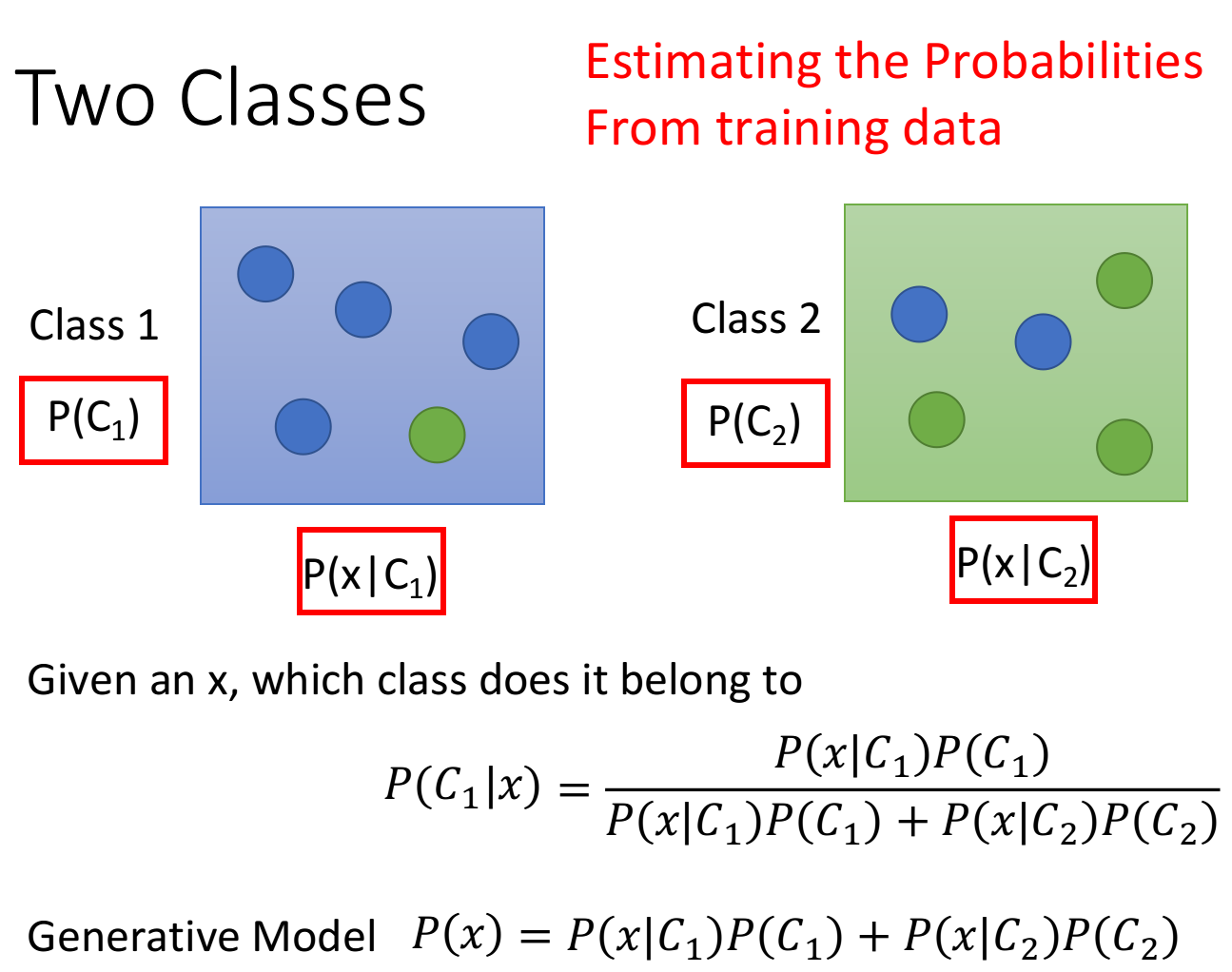
在半监督生成模型中，计算的公式会有相应的变化，其具体步骤如下：

随机初始化一组参数：$\theta=\begin {Bmatrix} P (C_1),P (C_2),u^1,u^2,\sum\end {Bmatrix}$
利用 model 计算每一笔 unlabeled data $x^u$ 属于 class1 的概率 $P_\theta (C_1|x^u)$
更新参数：

计算每个类别的概率：$P (C_1)=\frac {N_1+\sum _{x^u} P (C_1|x^u)}{N}$

计算每个类别的均值：$u_1=\frac {1}{N_1}\displaystyle\sum_{x^r\in C_1} x^r+\frac {1}{\sum_{x^u} P (C_1|x^u)}\displaystyle \sum_{x^u} P (C_1|x^u) x^u$

其他参数也可以用类似的方法得到
重复 2、3 步骤直至模型收敛

流程中的步骤 2 和步骤 3 即是 EM algorithm 中的 E 和 M

Low-density Separation

Low-density separation 方法的基础假设是：这个世界是非黑即白的，在两个类别的交界处数据的密度是很低的，因此两类数据之间会有明显的鸿沟

Self Training

先用 labeled data 训练一个模型 $f^*$, 可以使用任意的方法
然后用训练好的 $f^*$ 给 unlabeled data 打上标签
从 unlabeled data 中拿出一些 data 放入到 labeled data 中，选取的方法需要自定义
重复 1-3 的步骤

与 Generative Model 的区别：

Self Training 每一次选取的 unlabeled data 会强制给其打上标签，又称为 hard label。而生成模型会在每一次得到新模型的时候更新 unlabeled data 的 label 概率值，又称为 soft label。在生成模型中，是可以使用 soft label 的，这代表了这个样本对均值和方差的重要度影响；但是在神经网络的环境下，我们应该使用 hard label，因为这个 soft label 就是机器产生的，如果仍然以此作为目标 y，那么机器就学不到任何有用的信息了。

拓展知识 1：self-training 在回归任务上是否适用？

不适用。regression 并不像分类任务一样有一个 “决策边界”，所以当我们加入 unlabel data 的时候，拟合的函数 f * 并不会受到任何的影响。

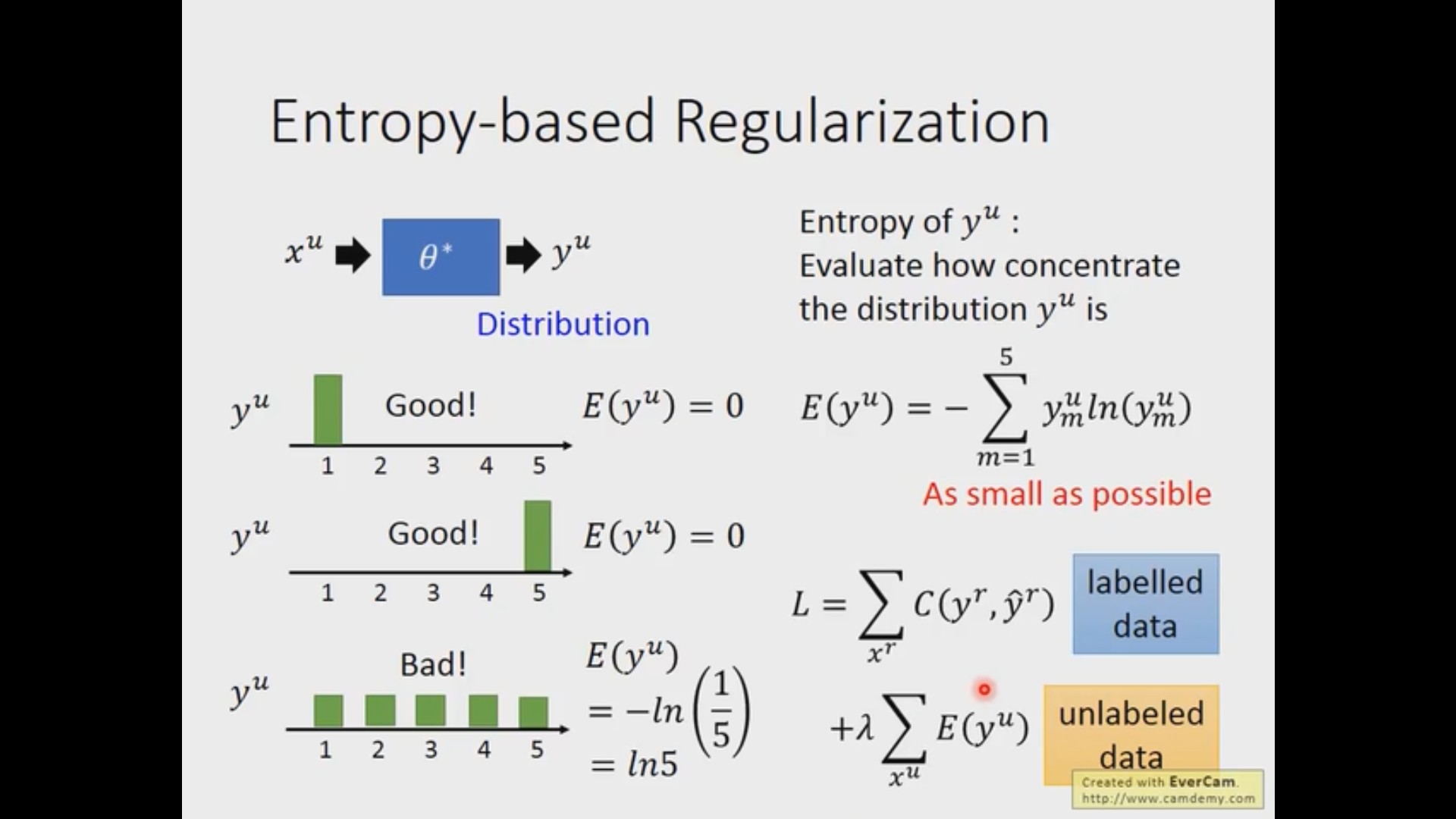
基于熵的正则化（Entropy-based Regularization）

因为我们的假设是这是一个非黑即白的世界，所以如果丢进来一个样本，我们希望可以和明确的给出他属于哪个类别（类似于 one-hot 的形式），而不是模糊的认为所有类别都是有可能的（每个类别取到平均概率）。而 “属于某个类别的概率很大，其他类别的概率很小” 这个概念可以使用信息熵来衡量，当每个类别的概率是均衡的时候，信息熵会取到最大值。而对于那些有标签的数据，我们还是使用传统的交叉熵损失，所以基于熵的方法更像是给原来的网络加入了一项正则项。

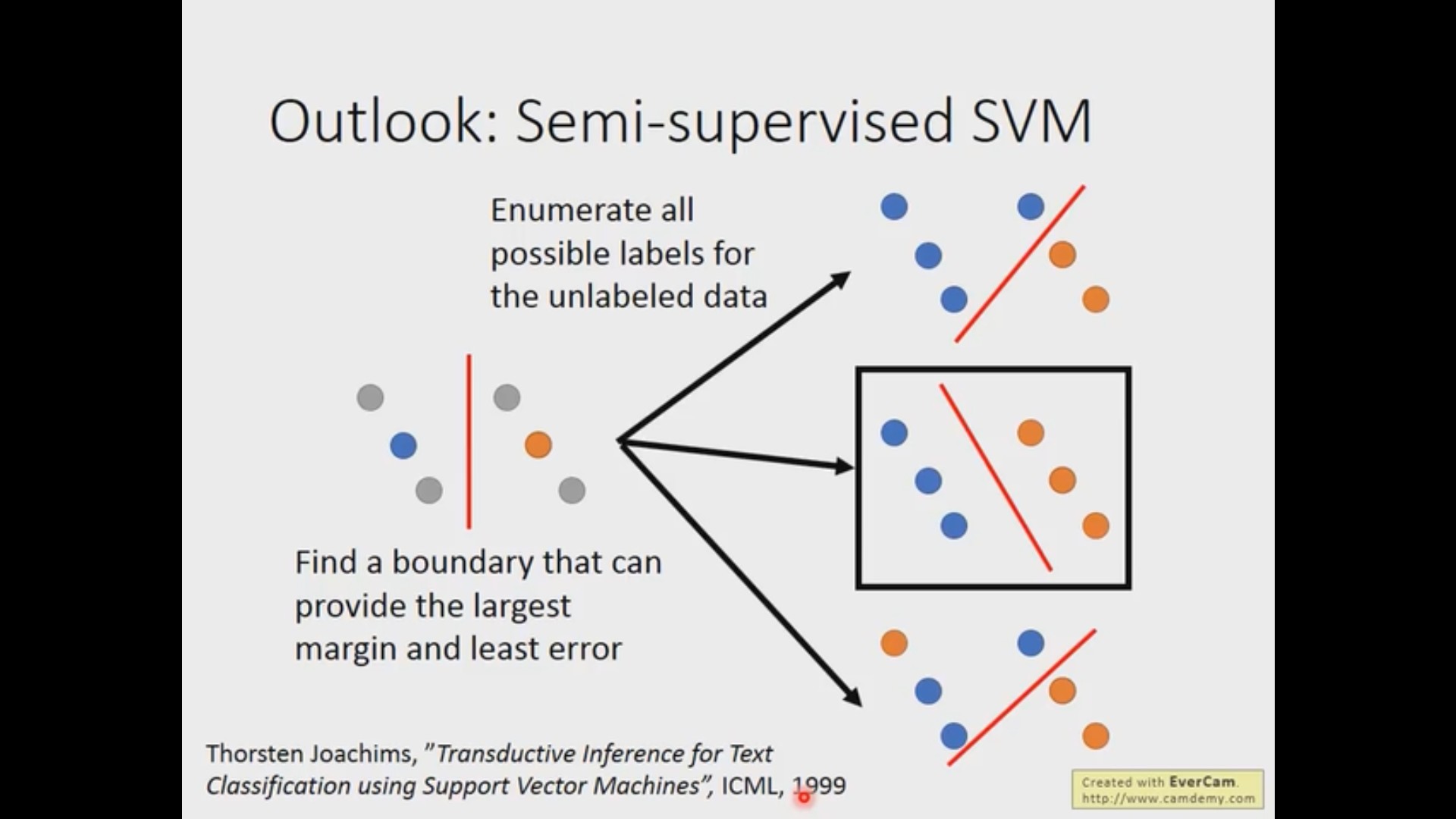
半监督 SVM（Semi-supervised SVM）

半监督 SVM 的想法是非常简单的，就是对于所有没有标签的样本，我们穷举所有的可能，对每一种可能使用 SVM 的方法，然后选取 margin 最大 loss 最小的那种可能。当然，穷举样本所有的可能是非常非常慢的，老师说原论文有给出解决方案，这一点以后用到的时候再去详细了解。

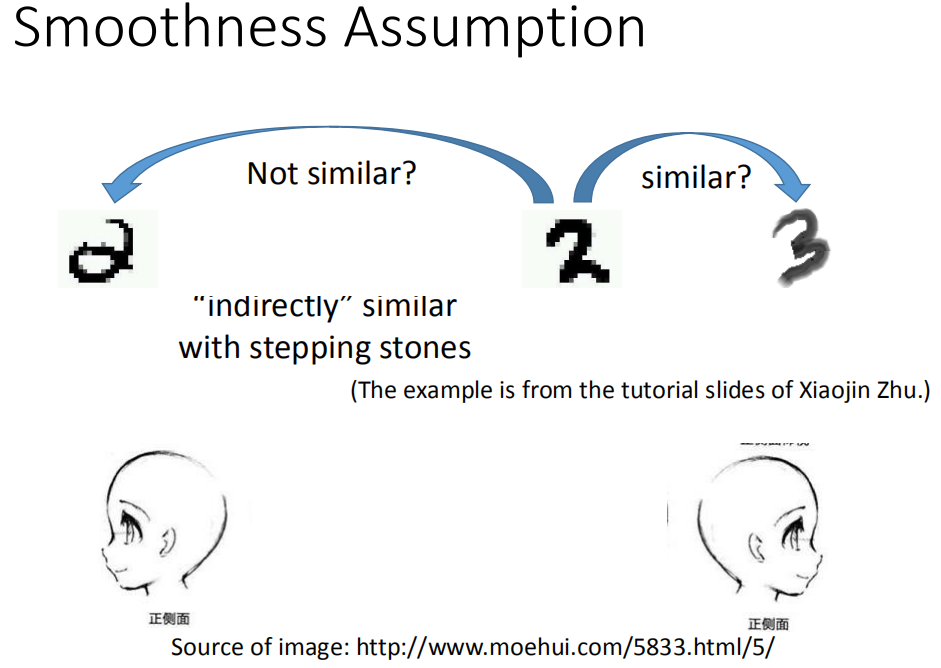
Smoothness Assumption

Smoothness Assumption 方法的基础假设是：近朱者赤，近墨者黑，即输入的两个 x 相似的时候，他们的输出也应该是相似的。所以这个问题的关键就在于，怎么衡量输入 x 的相似程度呢？

聚类和标记

最简单的方法就是套用聚类算法了，把聚类得到的一个类别中的所有的样本都看作是相似。
](https://s1.ax1x.com/2020/10/27/BQmYT0.png)

但是这个方法不一定有用，以图片为例子，单纯的使用 pixel 来判断样本的相似程度是不对的。

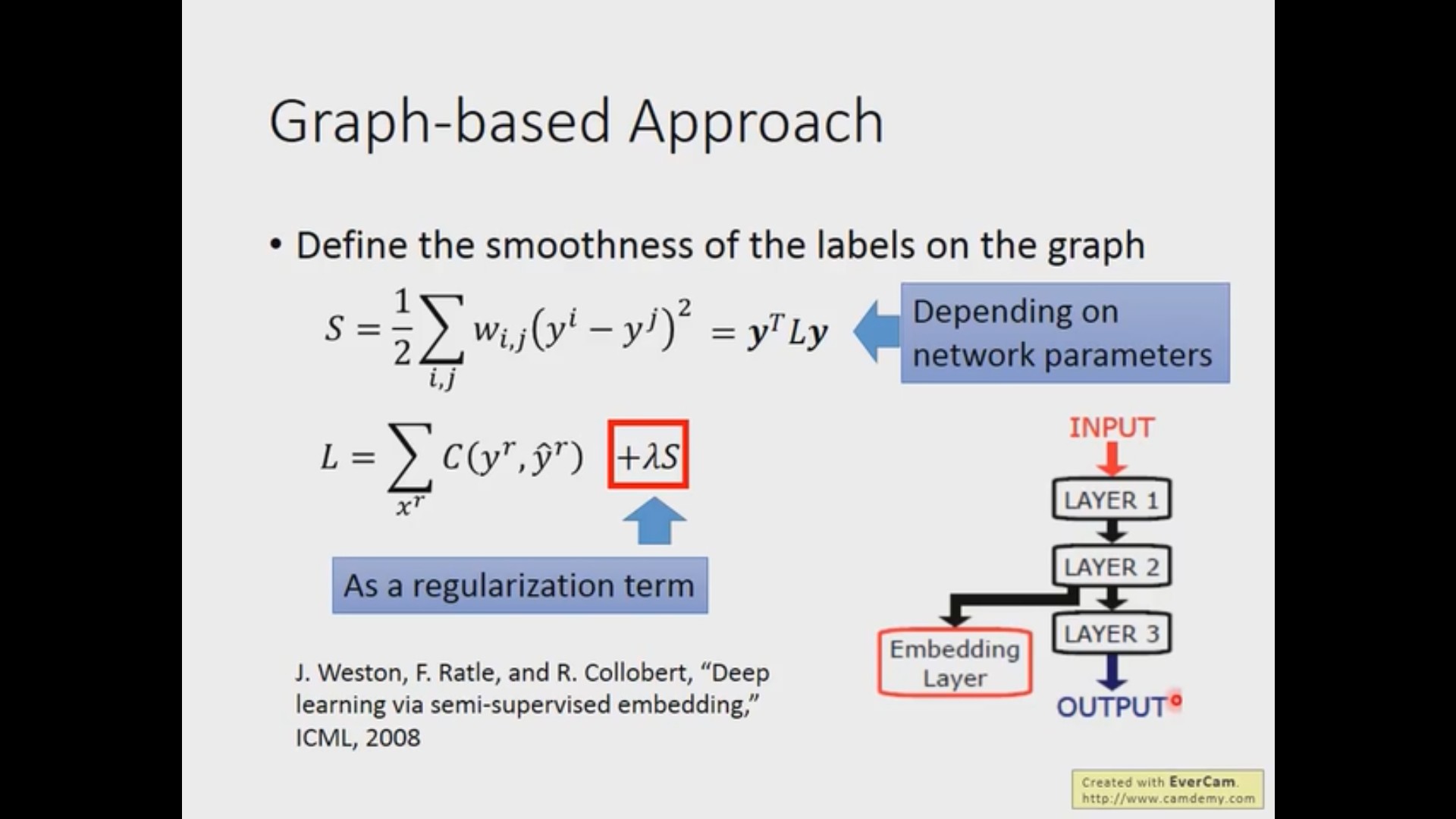
基于图的方法

首先也是类似的需要定义一个距离函数来计算两个样本之间的距离（相似度），然后可以用 K-nearest neighbor 或者 e-Beighborhood 的方法来加入边（这些边是可以加入 weight 属性的）。有了图之后，可以从有标签的样本出发对全局进行扩散从而对没有标签的样本进行分类。这种方法需要样本数量足够的大，否则同类样本之间会存在断层。